[프로젝트] C++ CUDA, Fast Fourier Transform을 이용한 이미지 블러
어떻게 이미지를 흐리게 만들 수 있을까요?
우리는 다양한 이미지 처리 프로그램에서, 주어진 이미지를 흐리게 만들 수 있습니다. 흐리다는 것은 수학적으로 어떻게 정의할 수 있을까요? 아마 가장 쉽고 직관적인 답변으로는 "해상도가 낮음"이 될 수도 있을 것 같습니다. 엄밀히 말해서 우리가 이번에 다룰 이야기와는 조금 거리가 있는 답변이긴 합니다만, 분명 그럴듯하죠. 그렇다면 해상도가 낮다는 것은 왜 흐리다는 것과 비슷한 의미를 지닐 수 있을까요?
현실은 연속적입니다. 우리가 무언가를 본다는 것은, 빛을 받아들인다는 것입니다. 물리 세계의 빛이라는 것에 '화질'이라는 개념이 존재할까요? 우리가 보는 화면에서 글씨의 픽셀은 분명 구분되어 있죠. 27인치 모니터에 희거나, 검거나 하는 것들이 200만여 개로 분리되어 있습니다. 물리적으로도 그럴까요? 물리적으로 픽셀은 단 하나의 무언가는 아닙니다. 그냥 연속적인 빛일 뿐이죠.
즉, 우리는 연속적인 현실의 무언가를 샘플링해서 봅니다. 만약 샘플링된 것이 현실의 무언가를 재현할 수 있을 정도라면, 우리는 '선명하다'고 느끼죠. 하지만 그렇지 않다면, '흐릿하다'고 느낍니다. 예를 들어, 다음 그림은 주기가 빠른 파동을 샘플링하였지만, 샘플링의 주기가 부적절해 마치 다른 파동처럼 보입니다.
즉 우리가 '흐릿하다'고 느끼는 것은, 실제의 디테일을 추측하기 어렵다는 것과 같은 이야기일 것입니다. 반대로, 샘플의 디테일을 일부러 뭉갠다면 그것은 흐릿하게 보이는 요인이 되지 않겠어요?
컨볼루션(Convolution)
컨볼루션은 수학의 한 연산입니다. 우리 전공자들은 인공지능으로 인해서 더욱 익숙하죠. 다만 주의하세요! 인공지능에서 이야기하는 컨볼루션은 사실 신호 처리 분야에서 사용하는 일반적인 컨볼루션 연산과 의미적으로 약간 다릅니다. 반전되지 않는다든가 하는 문제가 있죠. 하지만 그것은 중요치 않으므로 넘어가도록 하겠습니다.
컨볼루션은 쉽게 말해 한 신호를 슬라이딩해가면서 적분을 하는 것입니다. 다음 예제를 참고해보세요. 파란색의 신호를 움직이면서 해당하는 빨간 점과의 곱을 더해서 새롭게 신호를 만듭니다. 보통 파란색의 신호를 '커널(kernel)'이라고 부릅니다.
이러한 컨볼루션은 각 지점의 정보를, 주변의 정보와 함께 다시 갱신시킬 수 있습니다. 위의 예제에서도 특정 시점에서 값이 순간적으로 튀던 빨간색의 그래프와는 달리, 새롭게 컨볼루션된 그래프는 그것이 부드러워진 것을 볼 수 있죠.
우리는 이를 이용해서 이미지의 각 픽셀을 주변의 정보와 함께 섞어낼 수 있습니다. 이는 곧, 원본 이미지의 디테일을 삭제한다는 것이며, 이미지를 흐리게 만든다는 것입니다.
CPU를 이용한 이미지 컨볼루션 구현
우리는 컨볼루션 곱을 수행하는 코드를 생각해볼 수 있습니다. 임의의 이미지 각 픽셀에서 임의의 커널을 슬라이드 하면서 그 곱을 연산 후 합해야 합니다. 따라서 커널의 좌표와 이미지의 좌표를 매핑할 수 있어야 합니다. 다음은 이미지의 (r,c) 좌표에서 컨볼루션을 할 때, 커널의 (rk, ck)좌표와 이미지의 (ri, ci)좌표가 어떻게 정의되는지를 보입니다: 가령 (3,2)의 컨볼루션 곱에서 이미지의 (2,1) 좌표는 커널의 (0,0) 좌표가 됩니다. 이는 rk = 2 - 3 + 1, ck = 1 - 2 + 1이기 때문입니다.
이를 기반으로 함수를 만들 수 있습니다. 함수의 입력은 순서대로 다음과 같습니다: 입력 이미지, 이미지의 너비, 이미지의 높이, (정방형)커널, 커널의 높이 혹은 너비, 한 픽셀당 정보의 양, 출력 주소.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 | void convolution_cpu( const uint8_t* image_in, const int width, const int height, const float* kernel, const int kernel_size, const int bpp, uint8_t* image_out ) { for (int x = 0; x < width; x++) { for (int y = 0; y < height; y++) { for (int channel = 0; channel < bpp; channel++) { float sum = 0.f; const int radius = kernel_size / 2; for (int k_row = -radius; k_row <= radius; k_row++) { for (int k_col = -radius; k_col <= radius; k_col++) { int x_index = x + k_col; if (x_index < 0 || x_index >= width) continue; int y_index = y + k_row; if (y_index < 0 || y_index >= height) continue; int kernel_index = (k_row + radius) * kernel_size + (k_col + radius); int image_index = (x_index + y_index * width) * bpp + channel; sum += kernel[kernel_index] * (float)(image_in[image_index]); } } image_out[(y * width + x) * bpp + channel] = sum; } } } } | cs |
위 코드에는 반복문이 총 5개가 들어갑니다. 이미지의 가로, 세로를 순회하기 위한 반복문과 각 픽셀이 R,G,B,A 값 등을 가질 수 있으므로 이를 처리하는 반복문, 마지막으로 커널의 가로 세로를 순회하기 위한 반복문입니다. 이미지와 커널은 1차원으로 처리됨에 주의하세요!
커널을 순회할 때는 해당 픽셀이 이미지를 벗어나는지 확인하게 되며, 만약 벗어나지 않는다면 해당하는 커널과 이미지의 픽셀을 곱해 sum에 더합니다. 이후 sum의 결과는 출력 이미지의 픽셀값이 됩니다.
반복문이 5개라니, 인간적으로 너무하지 않나요?
맞습니다. 컬러 4K 이미지를 5x5 커널로 컨볼루션할 때 계산되는 시간복잡도는 대략 8억입니다. 단 하나의 이미지를 단순히 흐리게 만들기 위해서 10초를 기다려야 한다면 그것은 분명 문제일 것입니다.
이런 문제의 멋진 해결책이 있습니다. 바로 병렬화하는 것입니다. 각 픽셀을 커널과 곱하는 것은 서로 독립적인 연산입니다. 제가 (32,17) 픽셀의 출력값을 알기 위해서, (71,43) 픽셀의 출력값을 먼저 계산해야 하는 것은 아니라는 의미죠. 우리는 다들 최고의 병렬 처리 하드웨어를 지니고 있죠. 바로 GPU입니다.
GPU를 이용한 이미지 컨볼루션 구현
CUDA를 활용해봅시다. CUDA를 활용하기 위해서 GPU의 메모리에 필요한 공간들을 할당해주어야 합니다. cudaMalloc()을 이용해 필요한 메모리들을 할당하고, convolution_gpu_naive0() 함수를 호출해줍니다. 이때 GPU들의 코어를 효율적으로 활용하기 위해 적절한 gird와 threads값을 설정하여 호출합니다. 마지막으로, GPU 메모리 공간에 있는 결괏값을 CPU 메모리 공간으로 복사합니다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 | void convolution_gpu_naive( const uint8_t* image_in, const int width, const int height, const float* kernel, const int kernel_size, const int bpp, uint8_t* image_out ) { uint8_t* d_input_image = nullptr; uint8_t* d_output_image = nullptr; float* d_kernel = nullptr; const int image_size = width * height; cudaMalloc((void**)&d_input_image, sizeof(uint8_t) * image_size * bpp); cudaMalloc((void**)&d_output_image, sizeof(uint8_t) * image_size * bpp); cudaMalloc((void**)&d_kernel, sizeof(float) * kernel_size * kernel_size); checkCudaErrors(cudaMemcpy(d_input_image, image_in, sizeof(uint8_t) * image_size * bpp, cudaMemcpyHostToDevice)); checkCudaErrors(cudaMemcpy(d_kernel, kernel, sizeof(float) * kernel_size * kernel_size, cudaMemcpyHostToDevice)); int blocksx = ceil((image_size) / 256.0f); dim3 threads(256); dim3 grid(blocksx); convolution_gpu_naive0 << <grid, threads >> > (d_input_image, width, height, d_kernel, kernel_size, bpp, d_output_image); checkCudaErrors(cudaDeviceSynchronize()); cudaMemcpy(image_out, d_output_image, sizeof(uint8_t) * height * width * bpp, cudaMemcpyDeviceToHost); cudaFree(d_input_image); cudaFree(d_output_image); cudaFree(d_kernel); } | cs |
실질적으로 GPU 코어들에서 병렬적으로 동작하는 convolution_gpu_naive0()는 다음과 같습니다:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 | __global__ void convolution_gpu_naive0( const uint8_t* image_in, const int width, const int height, const float* kernel, const int kernel_size, const int bpp, uint8_t* image_out ) { const int size = width * height; unsigned tid = blockIdx.x * blockDim.x + threadIdx.x; const int x = tid % width; const int y = tid / width; if (tid >= size) return; const int radius = kernel_size / 2; for (int channel = 0; channel < bpp; channel++) { float sum = 0; for (int k_row = -radius; k_row <= radius; k_row++) { for (int k_col = -radius; k_col <= radius; k_col++) { int x_index = x + k_col; if (x_index < 0 || x_index >= width) continue; int y_index = y + k_row; if (y_index < 0 || y_index >= height) continue; int kernel_index = (k_row + radius) * kernel_size + (k_col + radius); int image_index = (x_index + y_index * width) * bpp + channel; sum += kernel[kernel_index] * (float)(image_in[image_index + 0]); } } image_out[tid * bpp + channel] = sum; } } | cs |
blockIdx,와 threadIdx를 이용해 해당 스레드의 논리적 순서를 얻을 수 있습니다. 이 순서를 이용해서 각각의 스레드가 서로 다른 픽셀에 대해서 병렬적으로 컨볼루션 곱을 수행할 수 있습니다.
이렇게 병렬처리를 수행할 시, 각각의 픽셀에 대한 시간복잡도가 상당히 줄어들게 됩니다. GPU 코어의 수는 많게는 2만 개 가까이 되므로, 상당히 성능을 올릴 수 있죠. 그런데도 여전히 문제는 존재합니다. 커널을 각 픽셀과 곱하는 연산은 병렬적으로 수행할 수 없다는 것이죠.
Fourier Transform
모든 그래프는 임의의 다항식의 합으로 나타낼 수 있다는 철학이 있습니다. 바로 테일러 급수에서 나오는 철학입니다. 이와 대비되는 것이 있는데요. 모든 그래프를 파동의 합으로 나타낼 수 있다는 것입니다. 바로 푸리에 변환입니다. 특정한 그래프를 푸리에 변환하는 것을, 우리는 공간(혹은 시간) 영역에서 주파수 영역으로 변환한다고도 말합니다. 쉽게 말하면, 선형대수학에서 기저를 변경하는 것과 마찬가지인 셈이죠.
 |
이러한 푸리에 변환을 이용해서 멋진 일들을 수행할 수 있습니다. 그중 하나가 바로 컨볼루션입니다. 컨볼루션 정리에 따르면, 주파수 영역에서의 곱은 공간 영역에서의 컨볼루션 연산과 같습니다. 즉, 신호와 커널을 공간 영역에서 주파수 영역으로 변환하고, 주파수 영역에서 그 둘을 곱한 뒤, 다시 주파수 영역에서 공간 영역으로 변환하면 컨볼루션된 값을 얻을 수 있다는 의미입니다.
우리는 이미지와 같이 무한한 신호의 파동이 아니더라도 푸리에 변환을 수행할 수 있습니다. 생각을 조금만 전환해보면 되죠. 바로 이미지를 반복되는 복잡한 파동으로 생각하는 것입니다. 커널도 마찬가지죠. 이를 이산 푸리에 변환이라고 합니다.
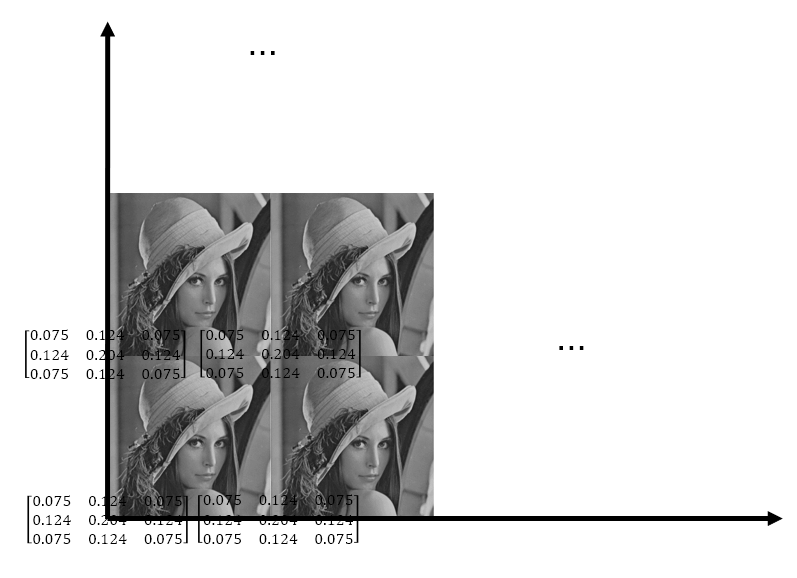
그렇다면 우리는 다음 그림처럼 커널과 이미지의 컨볼루션 연산을, 주파수 영역에서 서로를 곱하는 것으로 생각해볼 수 있습니다:
곱한다는 것은 결국 같은 위치의 값들끼리 곱하는 것이므로, 다음처럼 겹쳐진 값들을 곱하는 것이 되겠죠. 하지만 무한하게 반복되는 파동을 무한하게 곱할 수 없습니다. 당연히 그럴 필요도 없죠. 어차피 반복되는 주기를 지닌 파동이기 때문입니다. 따라서 우리는 단 하나의 파동 주기만 봐야 합니다. [-π,π]를 볼 수도 있고, [0,2π]를 볼 수도 있습니다. 다음 그림의 경우, [0, 2π]를 봤습니다.
우리는 이미지 영역에 있는 값들을 다뤄야 합니다. 이 경우 커널만을 보면, 이미지의 각 모서리에 빨간색으로 표시된 커널들이 흩뿌려져 있는 것을 볼 수 있습니다. 3x3으로 작았던 커널을, 이미지의 크기에 맞게 키워주고 나머지는 0으로 채워주는 작업이 필요합니다. 이를 커널 패딩이라고 합니다.
다음은 커널을 패딩하는 코드입니다. 이 역시 병렬적으로 수행될 수 있으므로, CUDA를 이용해 연산합니다:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 | __global__ void pad_kernel( cufftReal* kernel_input, const int image_width, const int image_height, const int kernel_size, cufftReal* kernel_output) { unsigned int thread_index = blockIdx.x * blockDim.x + threadIdx.x; const int size = image_width * image_height; if (thread_index >= size) return; const int min_radius = kernel_size / 2; const int max_radius = kernel_size - min_radius; const int x = thread_index % image_width; const int y = thread_index / image_width; const bool is_x_left = x < max_radius; const bool is_x_right = x >= image_width - min_radius; const bool is_y_up = y < max_radius; const bool is_y_down = y >= image_height - min_radius; if (is_x_left && is_y_up) { const int kernel_y = min_radius + y; const int kernel_x = min_radius + x; int offset = kernel_y * kernel_size + kernel_x; kernel_output[thread_index] = kernel_input[offset]; return; } if (is_x_right && is_y_up) { const int kernel_y = min_radius + y; const int kernel_x = x - (image_width - min_radius); int offset = kernel_y * kernel_size + kernel_x; kernel_output[thread_index] = kernel_input[offset]; return; } if (is_x_left && is_y_down) { const int kernel_y = y - (image_height - min_radius); const int kernel_x = min_radius + x; int offset = kernel_y * kernel_size + kernel_x; kernel_output[thread_index] = kernel_input[offset]; return; } if (is_x_right && is_y_down) { const int kernel_y = y - (image_height - min_radius); const int kernel_x = x - (image_width - min_radius); int offset = kernel_y * kernel_size + kernel_x; kernel_output[thread_index] = kernel_input[offset]; return; } kernel_output[thread_index] = 0.f; } | cs |
주파수 영역에서의 곱
주파수 영역에서는 복소수로 값을 다룹니다. 이는 파동의 성분을 허수로 표현하는 것이 용이하기 때문입니다. 주파수 영역에서의 이미지와 커널을 곱해야 하므로, 이에 대한 함수 역시 정의할 필요가 있습니다.
1 2 3 4 5 6 7 8 9 10 11 12 | __global__ void pointwise_product(cufftComplex* a, cufftComplex* b, int size, float weight) { unsigned thread_index = blockIdx.x * blockDim.x + threadIdx.x; if (thread_index >= size) return; float a_real_original = a[thread_index].x; a[thread_index].x = a[thread_index].x * b[thread_index].x - a[thread_index].y * b[thread_index].y; a[thread_index].y = a_real_original * b[thread_index].y + a[thread_index].y * b[thread_index].x; a[thread_index].x *= weight; a[thread_index].y *= weight; } | cs |
고속 푸리에 변환을 할 준비를 전부 마쳤습니다.
고속 푸리에 변환에는 다양한 알고리즘이 있으며, 저 역시 이 부분에 대해서 자세히 알지 못하므로 설명은 생략합니다. CuFFT 라이브러리는 고속 푸리에 변환을 지원합니다. 이를 이용해서 시간복잡도를 효율적으로 줄일 수 있습니다. 다시 정리해보죠:
- 커널을 패딩합니다. (병렬 처리 가능)
- 이미지와 커널을 푸리에 변환합니다. (병렬 처리 가능)
- 주파수 영역의 이미지와 커널을 곱합니다. (병렬 처리 가능)
다음은 이를 수행하는 코드입니다:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 | void ConvolutionCalculator::convolution_cufft( const uint8_t* image_in, const float* kernel, const int image_width, const int image_height, const int kernel_width, const int kernel_height, const int bpp, uint8_t* image_out ) { const int image_size = image_width * image_height * bpp; const int image_real_size = image_width * image_height; const int kernel_size = kernel_width * kernel_height; const int complex_size = (image_width / 2 + 1) * image_height; uint8_t* d_int8_image = nullptr; checkCudaErrors(cudaMalloc((void**)&d_int8_image, image_size * sizeof(uint8_t))); checkCudaErrors(cudaMemcpy(d_int8_image, image_in, image_size * sizeof(uint8_t), cudaMemcpyHostToDevice)); cufftReal* d_real_kernel = nullptr; checkCudaErrors(cudaMalloc((void**)&d_real_kernel, kernel_size * sizeof(cufftReal))); checkCudaErrors(cudaMemcpy(d_real_kernel, kernel, kernel_size * sizeof(cufftReal), cudaMemcpyHostToDevice)); cufftReal* d_real_kernel_padded = nullptr; checkCudaErrors(cudaMalloc((void**)&d_real_kernel_padded, image_real_size * sizeof(cufftReal))); checkCudaErrors(cudaDeviceSynchronize()); int blocksx = ceil((image_real_size) / 256.0f); dim3 threads(256); dim3 grid(blocksx); pad_kernel << <grid, threads >> > (d_real_kernel, image_width, image_height, kernel_width, d_real_kernel_padded); checkCudaErrors(cudaDeviceSynchronize()); cufftHandle plan_kernel_to_complex; checkCudaErrors(cufftPlan2d(&plan_kernel_to_complex, image_height, image_width, CUFFT_R2C)); cufftComplex* d_complex_kernel = nullptr; checkCudaErrors(cudaMalloc((void**)&d_complex_kernel, complex_size * sizeof(cufftComplex))); cufftExecR2C(plan_kernel_to_complex, d_real_kernel_padded, d_complex_kernel); checkCudaErrors(cudaDeviceSynchronize()); for (int i = 0; i < bpp; i++) { cufftReal* d_real_image = nullptr; checkCudaErrors(cudaMalloc((void**)&d_real_image, image_real_size * sizeof(cufftReal))); collect_data << <grid, threads >> > (d_int8_image, bpp, i, image_real_size, d_real_image); checkCudaErrors(cudaDeviceSynchronize()); cufftComplex* d_complex_image = nullptr; checkCudaErrors(cudaMalloc((void**)&d_complex_image, complex_size * sizeof(cufftComplex))); checkCudaErrors(cudaMemset(d_complex_image, 0, complex_size * sizeof(cufftComplex))); checkCudaErrors(cudaDeviceSynchronize()); cufftHandle plan_image_to_complex, plan_result_to_real; checkCudaErrors(cufftPlan2d(&plan_image_to_complex, image_height, image_width, CUFFT_R2C)); checkCudaErrors(cufftExecR2C(plan_image_to_complex, d_real_image, d_complex_image)); checkCudaErrors(cudaDeviceSynchronize()); pointwise_product << <grid, threads >> > (d_complex_image, d_complex_kernel, complex_size, 1.0f / (image_width * image_height)); checkCudaErrors(cudaDeviceSynchronize()); checkCudaErrors(cufftPlan2d(&plan_result_to_real, image_height, image_width, CUFFT_C2R)); checkCudaErrors(cufftExecC2R(plan_result_to_real, d_complex_image, d_real_image)); write_data_to_image << <grid, threads >> > (d_int8_image, bpp, i, image_real_size, d_real_image); checkCudaErrors(cudaDeviceSynchronize()); cudaFree(d_real_image); cudaFree(d_complex_image); cufftDestroy(plan_image_to_complex); cufftDestroy(plan_result_to_real); } cufftDestroy(plan_kernel_to_complex); checkCudaErrors(cudaMemcpy(image_out, d_int8_image, image_size * sizeof(uint8_t), cudaMemcpyDeviceToHost)); cudaFree(d_real_kernel); cudaFree(d_real_kernel_padded); cudaFree(d_complex_kernel); cudaFree(d_int8_image); checkCudaErrors(cudaPeekAtLastError()); } | cs |
이러한 작업이 의미가 있는지 확인해야겠죠?
먼저, 일반적인 CPU 연산과 일반적인 GPU 연산의 비교는 다음과 같습니다. 가로축은 이미지의 크기, 세로축은 연산에 소모된 초 단위 시간입니다:
둘째로, 일반적인 GPU 연산과 고속 푸리에 변환을 활용한 GPU 연산의 비교는 다음과 같습니다:
본 프로젝트는 대학교 수업으로 2022년 하반기에 약 5주 동안 4명의 인원이 진행하였으며, 그중 타인이 관여하지 않은 내용에 관해서만 기술하였습니다.
끝.












댓글
댓글 쓰기