{{ label!='' ? 'Label : ' : (q!='' ? '검색 : ' : '전체 게시글') }} {{ label }} {{ q }} {{ ('('+(pubs|date:'yyyy-MM')+')') }}

[코딩의탑] 2층: 포탈(Portal)

포탈이란 무엇인가요?

  수많은 게임 팬들을 환호하게 만든 센세이셜한 게임이 있습니다: 바로 밸브 사의 포탈이죠. 포탈은 서로 다른 두 공간을 이어주는 문입니다. 플레이어는 포탈을 통과해 공간을 이동할 수 있고, 통과하지 않아도 맞은 편의 공간을 볼 수 있죠. 또한, 포탈을 통과할 때는 운동량이 보존됩니다. 공중에서 빠른 속도로 낙하하면서 땅바닥에 열려 있는 포탈을 통과하게 되면, 맞은편 포탈로 대포알처럼 튕겨나갈 수 있다는 것이죠!

<Portal>

  코딩의 탑 2층에서 우리는 이러한 포탈의 구현을 다루게 될 것입니다.


어떻게 해결할 수 있을까요?

  우리는 다음 두 가지 작은 목표를 해결해나갈 것입니다.

  • 임의의 좌표계의 벡터를, 다른 임의의 좌표계로 변환할 수 있습니다.
  • 사원수(Quaternion)를 이용하여, 두 좌표계의 차이만큼 회전시킬 수 있습니다.


준비운동을 시작해 보자구요..

기저

  우리는 좌표 공간에 벡터를 표현하죠. 이 때의 축은 각각 x축, y축, z축이 됩니다. 사실 이 축들은 곧 기저 벡터입니다. 기저 벡터라 함은, 벡터 공간에서 임의의 벡터를 표현하는데 쓸 수 있는 벡터들입니다. 기저 벡터가 x축, y축, z축의 단위 벡터라면 이는 다음과 같이 표현해볼 수 있겠죠: x(1,0,0), y(0,1,0), z(0,0,1).

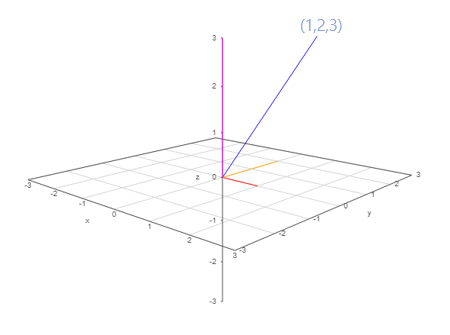
  이 세 가지 벡터만 있다면, 3차원의 모든 벡터를 표현할 수 있습니다. 가령 (1,2,3)은 1*x+2*y+3*z로 표현해볼 수 있습니다. 다음 그림을 참고해보세요:


  재미있는 사실은 이러한 기저 벡터들은 우리가 원하는 대로 얼마든지 만들 수 있다는 것입니다. 심지어, 다른 기저 벡터의 표현으로도 변환해볼 수 있죠! 그러기 위해, 우리는 행렬식을 이용해 벡터의 표현을 일반화해볼 수 있습니다. 다음 그림을 참고해보세요: i, j, k는 각 기저의 성분이 되며, (x1, y1, z1), (x2, y2, z2), (x3, y3, z3)는 기저 벡터이고 크기가 1입니다.


벡터의 표현

  우리는 포탈을 구현하므로, 반대편에 있는 포탈의 좌표 정보들을 이용해 눈 앞에 그것들을 재현해야 합니다. 우리가 알고 있는 것은 반대편의 포탈이 어떻게 놓여있는지(기저 벡터)와, 다양한 물체들의 좌표들 뿐입니다. 그리고 우리가 알고 싶은 것은 반대편의 포탈과 다른 물체들 간의 관계, 즉 i, j, k가 됩니다. 이는 역행렬을 이용해서 손쉽게 구할 수 있습니다.


  곧, 각 기저의 성분을 구해냈으니, 다른 포탈의 기저가 있다면 이를 이용해서 변환된 좌표를 얻어낼 수 있습니다:


  

사원수(Quaternion)

  사원수에 대해서는 자세히 설명드리기 어렵습니다. 제 수학적 이해가 부족하기 때문이죠. 하지만 간략하게나마 설명을 드리려고 합니다.

  수학적으로 회전은 무엇일까요? 회전은 곧 크기가 변하지 않는 연산입니다. 크기가 변하지 않는 연산으로 바로 생각나는 것이 있죠. 바로 1을 곱하는 것입니다. 우리는 실수에서도 회전을 해볼 수 있습니다. -1을 곱하면, 수직선 상에서 180도 회전하는 셈이죠.

  수학에서 회전을 훌륭하게 해내는 수가 있습니다. 바로 허수입니다. 허수는 제곱하였을 때 음수가 나오는 수를 의미합니다. 회전이야말로 허수의 존재 이유라고 말할 수 있죠. 실수부와 허수부를 갖는 복소수를 복소 평면에 시각화하면, 우리는 회전을 손쉽게 할 준비를 마친 것입니다. 복소 평면은 x축은 실수부, y축은 허수부로 표현한 평면입니다. 가령 (1, 2)은 1+2i와 같습니다.

  허수 i는 제곱을 하면 -1이 됩니다. 이를 토대로 i를 곱하는 시행을 반복적으로 시도해봅시다:

  • 0번째 시행: 1
  • 1번째 시행: i
  • 2번째 시행: -1
  • 3번째 시행: -i
  • 4번째 시행: 1

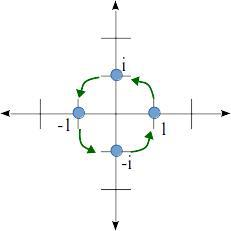
  4번째 시행 때, 우리는 다시 1로 되돌아 왔습니다. 이를 복소평면에 시각화해보죠:


  어떤가요? 복소 평면에서 i를 곱하는 것은 마치 90도 회전하는 것과 같습니다. 회전 시 크기는 절대 변하지 않음을 확인하세요. 크기가 변하지 않은 이유는, i 역시 복소 평면에서 크기가 1이기 때문입니다. 크기가 1인 수를 곱하면 크기는 절대 변하지 않죠.

  하지만 이는 평면의 회전에 불과하죠. 심지어 실수부만 보았을 때, 이는 여전히 1차원의 회전에 불과합니다. 이러한 회전을 3차원의 공간에서 수행할 수 있게 해주는 것이 바로 사원수의 개념입니다.


  사원수는 4개의 수로 회전을 표현합니다. 실수인 w와 허수인 x, y, z입니다. 회전은 크기가 1인 사원수를 곱하는 것이죠. 이는 머릿속으로 쉽게 납득갈만한 개념들은 아닙니다. 다만 이를 통해서 손쉽게 회전을 해낼 수 있다는 것과, 다양한 공식들을 이용해 우리가 원하는 결과를 도출해낼 수 있다는 것이 중요합니다.


본격적으로 시작해봅시다!

  먼저 포탈을 타고 이동하는 것부터 구현해봅시다. 포탈을 타고 이동한다는 것은 좌표가 변한다는 것입니다. 이 때, 우리는 다양한 것들을 함께 변화시켜주어야 합니다.

  • 당연히, 포탈을 탄 객체의 좌표
  • 포탈을 탄 객체의 속도
  • 포탈을 탄 객체의 회전

  포탈을 탄 객체의 좌표는 단순히 포탈의 좌표가 되지는 않습니다. 포탈은 평면으로 존재하며, 평면의 어디로든 객체가 통과할 수 있기 때문입니다. 따라서 객체와 두 포탈 사이의 관계를 이용해 변환된 좌표를 도출해주어야 합니다.

  이는 곧 각 포탈을 각각의 3차원 좌표계의 기저로 생각해볼 수 있습니다. 포탈의 윗쪽 방향 벡터, 앞쪽 방향 벡터, 옆쪽 방향 벡터 3가지가 기저 벡터가 될 것입니다. 객체가 입구 포탈 좌표계에서의 기저 성분을 확인하고, 다시 이를 출구 포탈 좌표계의 기저로 곱해주면 될 것입니다. 이 때, 출구 포탈은 방향이 반대라는 사실에 주의하세요. 우리가 박수를 칠 수 있는 이유는 손이 반대로 생겼기 때문입니다. 이를 함수로 구현해보면 다음과 같습니다:


소스코드: Portal::ConvertVectorToOppositeSpace()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
Vector APortal::ConvertVectorToOppositeSpace(const FVector Point)
{
    const FVector PortalNormal = GetActorForwardVector();
    const FVector PortalRight = GetActorRightVector();
    const FVector PortalUp = GetActorUpVector();
 
    const FMatrix PortalBasis = FMatrix(
        PortalNormal, 
        PortalRight, 
        PortalUp, 
        FVector(0, 0, 0)
    );
    const FMatrix PortalBasisInverse = PortalBasis.Inverse();
    const FMatrix ActorLocationMatrix = FMatrix(
        Point, 
        FPlane(0, 0, 0, 0), 
        FPlane(0, 0, 0, 0), 
        FPlane(0, 0, 0, 0)
    );
    const FMatrix Component = ActorLocationMatrix * PortalBasisInverse;
 
    const FVector OppositeNormal = -(Link->GetActorForwardVector());
    const FVector OppositeRight = -(Link->GetActorRightVector());
    const FVector OppositeUp = Link->GetActorUpVector();
    const FMatrix OppositeBasis = FMatrix(
        OppositeNormal, 
        OppositeRight, 
        OppositeUp, 
        FVector(0, 0, 0)
    );
 
    const FMatrix Result = Component * OppositeBasis;
    return FVector(Result.M[0][0], Result.M[0][1], Result.M[0][2]);
}
cs

  FMatrix 생성 시 빈 값들을 넣어주는 이유는 언리얼 엔진4가 4x4 행렬을 기반으로 다루기 때문입니다. 

  이 함수를 이용해 우리는 원하는 벡터들을 맞은편 포탈의 좌표계로 변환할 수 있습니다. 회전도 마찬가지로 변환할 수 있어야겠죠. 회전은 사원수를 이용합니다. 


소스코드: Portal::ConvertQuatToOppositeSpace()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
FQuat APortal::ConvertQuatToOppositeSpace(FQuat Quat)
{
    FTransform SourceTransform = GetActorTransform();
    FTransform TargetTransform = Link->GetActorTransform();
 
    FQuat Diff = TargetTransform.GetRotation()
        * SourceTransform.GetRotation().Inverse();
    FQuat Result = Diff * Quat;
 
    // Turn 180 degrees
    FVector UpVector = TargetTransform.GetRotation().GetUpVector();
    FQuat Rotator = FQuat(UpVector.X, UpVector.Y, UpVector.Z, 0);
 
    return Rotator * Result;
}
cs

  쉽게, 각 포탈이 각자의 사원수를 지녔다(회전했다)고 생각해봅시다. 우리는 그 둘의 차이를 이용해서 객체를 회전시켜야 합니다. 우리는 이를 행렬처럼 연산해볼 수 있습니다.


  따라서 도출된 diff만큼 주어진 변수를 회전시킵니다. 다만, 출구 포탈의 경우 180도 회전한 셈이므로, 해당 출구 포탈의 윗쪽 방향 벡터를 기준으로 한 번 더 회전 시킵니다. 180도 회전의 경우, 원하는 축으로 사원수를 구성한 뒤 곱하면 됩니다.


  위 두 함수를 이용해서 객체를 순간이동해주는 함수를 만들어볼 수 있습니다. TeleportActor() 함수는 포탈에 들어온 객체를 인자로 받아 그를 맞은편 포탈로 이동시켜줍니다.


소스코드: Portal::TeleportActor()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
void APortal::TeleportActor(AActor* Target)
{
    // Convert position and velocity
    FVector ActorLocationOnOppositeSpace = ConvertVectorToOppositeSpace(
        Target->GetActorLocation() - GetActorLocation()
    );
    FVector VelocityOnOppositeSpace = ConvertVectorToOppositeSpace(
        Target->GetVelocity()
    );
    
    // Convert rotation
    FQuat QuatOnOppositeSpace = ConvertQuatToOppositeSpace(
        Target->GetActorQuat());
    
    // Set changes
    Target->SetActorRotation(QuatOnOppositeSpace);
    Target->SetActorLocation(
        Link->GetActorLocation() + ActorLocationOnOppositeSpace
    );
 
    ACharacter* Character = Cast<ACharacter>(Target);
    if (Character)
    {
        Character->GetMovementComponent()->Velocity = 
            VelocityOnOppositeSpace;
 
        AController* Controller = Character->GetController();
 
        FQuat ControllerQuat = 
            ConvertQuatToOppositeSpace(
                FQuat(Controller->GetControlRotation())
        );
 
        Character
            ->GetController()
            ->SetControlRotation(ControllerQuat.Rotator()
        );
    }
}
cs


위치, 운동량, 회전이 잘 변환되네요.


하지만 이래서야 맞은편 포탈이 지옥에 연결되어 있어도 알 길이 없잖아요!

  좋습니다. 이번엔 포탈 너머에 무엇이 있는지 플레이어에게 보여주도록 하죠. 우리는 반대편의 포탈에 플레이어와 똑같은 시야각을 갖는 카메라를 하나 두어서, 그 카메라의 시야를 보여주려고 합니다. 마치 포탈의 평면에는 CCTV가 연결되어 그 화면이 송출되는 것과 마찬가지죠. 이 역시 앞서 만든 함수들로 손쉽게 해결할 수 있습니다.


소스코드: Portal::UpdateCapture()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
void APortal::UpdateCapture()
{
    APlayerCameraManager* PlayerCamera = 
        GetWorld()->GetFirstPlayerController()->PlayerCameraManager;
    FVector CameraRelativeLocation = 
        PlayerCamera->GetCameraLocation() - GetActorLocation();
 
    FVector ConvertedCameraLocation = 
        ConvertVectorToOppositeSpace(CameraRelativeLocation);
    
    AController* Controller = 
        UGameplayStatics::GetPlayerController(GetWorld(), 0);
    FQuat ControllerQuat = 
        ConvertQuatToOppositeSpace(
            FQuat(Controller->GetControlRotation())
        );
 
    SceneCapture->SetWorldLocation(
        Link->GetActorLocation() + ConvertedCameraLocation
    );
    SceneCapture->SetWorldRotation(ControllerQuat);

    SceneCapture->CaptureScene();
}
cs


잘 된다 싶었더니, 덜컹거리네요.

웬 흰색 상자가 시야를 가려버리는군요.

  플레이어의 위치에 따라 카메라를 놓고 해당 시야를 보여주다보니 문제가 생겼습니다. 포탈과 카메라 사이에 오브젝트가 있으면 오브젝트에 가려져버린다는 것입니다. 다행히 이는 아주 간단하게 해결해낼 수 있습니다. 바로 클리핑(Clipping)이라는 기술을 이용해서 말이죠.

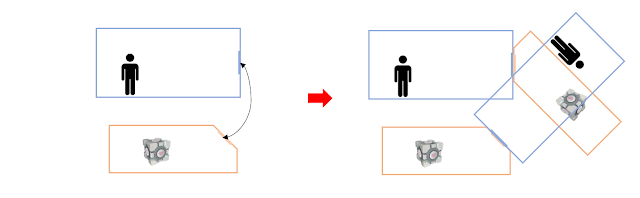
  우리가 특정한 카메라를 이용해 씬(Scene)의 객체들을 모니터의 화면에 투영시킬 때, 그래픽스 엔지니어는 다양한 문제들과 싸우고 있습니다. 그 중 하나는 클리핑의 문제입니다. 카메라와 특정한 오브젝트가 매우 가까운 거리로 붙어있거나, 오히려 뒤에 있으면, 이를 투영하는 과정에서 여러가지 문제의 여지가 생깁니다. 

Clipping

  따라서 카메라의 이미지 평면에 투영할 때, 클리핑이라는 기술을 이용해 투영할 오브젝트들을 필요에 따라 잘라냅니다. 우리는 이런 멋진 기술을 코드 몇 줄만으로 작성할 수 있습니다. 우리는 출구 포탈 평면 이전의 오브젝트들은 렌더링하지 않아도 됩니다.


소스코드: Portal::UpdateCapture() - 수정됨

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
void APortal::UpdateCapture()
{
    APlayerCameraManager* PlayerCamera = 
        GetWorld()->GetFirstPlayerController()->PlayerCameraManager;
    FVector CameraRelativeLocation = 
        PlayerCamera->GetCameraLocation() - GetActorLocation();
 
    FVector ConvertedCameraLocation = 
        ConvertVectorToOppositeSpace(CameraRelativeLocation);
    
    AController* Controller = 
        UGameplayStatics::GetPlayerController(GetWorld(), 0);
    FQuat ControllerQuat = 
        ConvertQuatToOppositeSpace(
            FQuat(Controller->GetControlRotation())
    );
 
    SceneCapture->SetWorldLocation(
        Link->GetActorLocation() 
        + ConvertedCameraLocation
    );
    SceneCapture->SetWorldRotation(ControllerQuat);
 
    // Clipping
    SceneCapture->ClipPlaneNormal = Link->GetActorForwardVector();
    SceneCapture->ClipPlaneBase = Link->GetActorLocation();
 
    SceneCapture->CaptureScene();
}
cs


사실, 간단하게 넘어간 문제가 있었습니다.

  사원수를 이용한 회전을 하더라도, 여전히 문제가 있을 수 있습니다. 포탈의 각도와 플레이어의 각도에 따라 플레이어의 Roll이 변할 수 있습니다. 30도 왼쪽으로 기울어진 포탈을, 땅바닥에 바로 서서 진입한다고 생각해보세요. 아마 출구에서 나올 때는 제가 기울어진 상태로 나올 것입니다. 우리는 이런 플레이어의 기울음을 바로잡을 필요가 있습니다.

어지러움 주의!


  간단히, 매 프레임마다 플레이어의 각도가 기울어져있으면 이를 바로잡도록 하였습니다. 부드럽게 바로잡기 위해서 약간의 장치를 더했죠.


소스코드: Character::Tick(), Character::GetRecoveryDelta()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
void ATowerOfCodePortalCharacter::Tick(float DeltaSeconds)
{
    Super::Tick(DeltaSeconds);
    float Threshold = 1.f;
 
    FRotator ControllerRotation = GetController()->GetControlRotation();
    FRotator NewControllerRotation = FRotator(
        ControllerRotation.Pitch, 
        ControllerRotation.Yaw, 
        ControllerRotation.Roll - GetRecoveryDelta(
            ControllerRotation.Roll, 
            RollRecoverySpeed, 
            Threshold)
    );
 
    FRotator ActorRotation = GetActorRotation();
    FRotator NewActorRotation = FRotator(
        ActorRotation.Pitch - GetRecoveryDelta(
            ActorRotation.Pitch, 
            RollRecoverySpeed, 
            Threshold), 
        ActorRotation.Yaw, 
        ActorRotation.Roll - GetRecoveryDelta(
            ActorRotation.Roll, 
            RollRecoverySpeed, 
            Threshold)
    );
 
    GetController()->SetControlRotation(NewControllerRotation);
    SetActorRotation(NewActorRotation);
}
 
float ATowerOfCodePortalCharacter::GetRecoveryDelta(float Target, float RecoverySpeed, float Threshold)
{
    float Delta = 0.f;

    if (FMath::IsNearlyEqual(RecoverySpeed, 0.f, 1e-5))
        return 0.f;

    if (Target > 180)
        Target -= 360;
    Delta = Target / (1.f / RecoverySpeed);
    if (FMath::Abs(Target) < Threshold)
    {
        Delta = Target;
    }
 
    return Delta;
}
cs


방금 여러분도 보이는 문제가 하나 더 있었죠?

  그렇습니다. 포탈 속의 포탈은 렌더링되지 않는다는 사실입니다. 이를 지나칠 순 없지만, 그래도 할말은 해야겠네요. 우리가 여지껏 달려온 방법을 뒤엎지 않는 이상, 언리얼 엔진4에서는 이를 해결할 쉬운 방법이 존재하지 않는다는 것입니다. 

  우리가 포탈 안의 세계를 렌더링하는 것은, 임의의 카메라를 하나 더 두어 그 장면을 캡처하는 것입니다. 언리얼 엔진4의 씬캡처 컴포넌트는 절두체(Frustum)을 이용한 일부분의 캡처를 지원하지 않습니다. 저 작은 포탈의 화면을 렌더링하기 위해 사실은 플레이어의 시야각과 똑같은 너비의 화면을 포탈의 좌표계에서 캡처하고, 그 중 대부분은 버리고 포탈 너머로 보이는 극히 일부분만 렌더링해주는 것이죠. 이는 비용이 결코 싸지 않습니다.

  포탈 속의 포탈을 렌더링하기 위해, 우리는 여지껏 했던 일들을 재귀적으로 처리해나가야 합니다. 하지만 화면 하나를 찍는 것은 굉장히 비싸죠. 5번만 재귀적으로 렌더링해도, 여러분은 모니터 5개에 동시 렌더링을 하는 것과 마찬가지입니다.

  이를 해결하려면 언리얼 엔진4의 내부적인 동작을 자세하게 알아야 합니다. 하지만 이 역시 저에겐 비용이 크군요. 어쨌거나, 성능을 포기하더라도 재귀적으로 렌더링해봅시다.


소스코드: Portal::UpdateCapture() - 수정됨, Portal::UpdateCaptureRecursive()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
void APortal::UpdateCapture()
{
    APlayerCameraManager* PlayerCamera = 
        GetWorld()->GetFirstPlayerController()->PlayerCameraManager;
    FVector CameraRelativeLocation = 
        PlayerCamera->GetCameraLocation() - GetActorLocation();
 
    if (FVector::DotProduct(
            CameraRelativeLocation, 
            PlayerCamera->GetActorForwardVector()
        ) > 0)
        return;
 
    SceneCapture->ClipPlaneNormal = 
        Link->GetActorForwardVector();
    SceneCapture->ClipPlaneBase = 
        Link->GetActorLocation();
 
    UpdateCaptureRecursive(
        CameraRelativeLocation, 
        FQuat(PlayerCamera->GetActorQuat()), 
        0
    );
}
 
void APortal::UpdateCaptureRecursive(
    FVector CameraRelativeLocation, 
    FQuat CameraQuat, 
    int Depth
)
{
    if (Depth > RecursionThreshold)
        return;
 
    FVector ConvertedCameraLocation =
        ConvertVectorToOppositeSpace(CameraRelativeLocation);
 
    FQuat ConvertedCameraQuat =
        ConvertQuatToOppositeSpace(CameraQuat);
 
    UpdateCaptureRecursive(
        Link->GetActorLocation() + ConvertedCameraLocation - GetActorLocation(), 
        ConvertedCameraQuat, 
        Depth + 1
    );
    SceneCapture->
        SetWorldLocation(
            Link->GetActorLocation() + ConvertedCameraLocation
        );
    SceneCapture->SetWorldRotation(ConvertedCameraQuat);
    HideActorsNotVisible();
    SceneCapture->CaptureScene();
    SceneCapture->ClearHiddenComponents();
}
cs

60프레임을 겨우 넘더군요.


드디어 완성했네요! 이젠 정말로 끝입니다.

멋진 포탈입니다!


  우리는 포탈을 구현해보았습니다. 벡터 공간의 기저와 사원수를 이용해 다양한 좌표계 전환 및 회전을 해볼 수 있었습니다. 

  이상으로, 코딩의 탑 2층의 모험을 마칩니다.


끝.

댓글

  1. rabbit2022년 7월 12일 오후 8:36

    흔하디 흔한 기본 포탈 수준이 아니라...

    1. 3인칭으로 바라봤을때 포탈에 몸이 반쯤 걸쳐있는 상황에 대한 처리 (메쉬 및 이펙트의 복제 처리)
    2. 포스트 프로세스나 Fog등이 포함된 상황에서의 처리
    3. 포탈의 사용 명세 (포탈의 뒷면에서 정면방향으로의 이동 제약 등)와 레벨 디자인적 고려사항
    4. 3인칭 카메라일 경우의 처리
    5. 멀티 씬 등 포탈 이동 시 스카이박스, 라이팅이 완전히 다른 경우의 처리
    6. 최적화

    요런 이슈도 고려해보시면 좋을 것 같습니다. ^^
    적어도 3번까지의 내용이 완벽하게 적용되지 않으면 게임에 포함되기 힘들거든요~

    답글삭제

댓글 쓰기

이 블로그의 인기 게시물

[코딩의탑] 4층: 툰 쉐이딩

이미지
가끔은 만화스러운 느낌이 좋을 때도 있죠.   셀 쉐이딩(Cel shading)이라고도 불리는 툰 쉐이딩 기법은 절제된 빛 표현으로 화면을 그리는 비사실적(non-photorealistic) 렌더링 기법 중 하나입니다.  <Borderlands 시리즈>   이러한 툰 쉐이딩은 다양한 방식으로 실현되고 있으며, 언리얼 엔진을 활용한 툰 쉐이딩 역시 어렵지 않습니다. 특히, 포스트 프로세싱을 이용하여 만화스럽게 후처리를 해주는 방법은 클라이언트 프로그래머들이 손쉽게 사용할 수 있는 방법입니다.   하지만, 포스트 프로세싱을 이용한 툰 쉐이딩은 다음과 같은 단점이 존재하는데요: 포스트 프로세싱 자체의 비용이 존재합니다. 특정한 머티리얼에만 툰 쉐이딩을 적용하기 어렵습니다. (커스텀 스텐실 버퍼를 활용하는 것이 대표적인 방법이며, 이는 개발자를 피곤하게 합니다)   따라서, 우리는 포스트 프로세싱을 활용하지 않는 툰 쉐이딩을 구현해보도록 하죠. 우리는 다음을 구현할 것입니다: 특정 물체의 윤곽선을 추가로 렌더링합니다. 특정 물체의 음영을 부드럽지 않은 단계별 음영으로 변경합니다. 이들의 사용 여부와 윤곽선 굵기, 색을 머티리얼 에디터 속성으로 결정할 수 있습니다. 반복되는 컴파일을 줄이기 위해 머티리얼 인스턴스로 만들 수 있으며, 윤곽선의 굵기를 재컴파일 없이 변경할 수 있습니다.   이는  언리얼 엔진 5의 소스를 직접 수정하는 방법임에 주의하세요. 이러한 방법 역시 마법이 아니므로, 비용이 존재합니다. 이는 차차 이야기하도록 하겠습니다. 그 전에 언리얼 엔진 5를 살펴보도록 하죠. 렌더링 패스 디퍼드 쉐이딩으로 렌더링에 필요한 다양한 정보를 담는 버퍼들   언리얼 엔진은 기본적으로 PC 게임에 한해 디퍼드 쉐이딩을 수행합니다. 디퍼드 쉐이딩이란 포워드 쉐이딩의 반대 개념입니다. 한 물체를 렌더링한다고 생각해보죠. 그 물체의 3차원 세계 좌표와 물체 표면의 법선, 표면 거칠기의 정도, 표면에 매핑된 텍스처와 변위 등 수많은 요소들을 고려해 우리 눈에 보
자세한 내용 보기

[코딩의탑] 3층: 바다 렌더링

이미지
바다를 그려봅시다.   수많은 게임들은 바다를 배경으로 하고 있습니다. 굳이 바다를 게임의 메인 배경으로 하지 않더라도, 게임 어느 중간에는 꼭 바다를 볼 수 있는 순간이 나오기 마련이죠.  <Sea of Thieves>   이러한 바다를 유체역학적 지식으로 구현하는 것은 쉽지 않습니다. 화면에 보이는 입자가 너무 많아 현실적으로 계산 능력이 부족하기 때문입니다. 따라서 많은 게임들은 바다를 구현하기 위해서 수많은 편법을 활용하고 있습니다. 대표적인 방법은 Displacement Mapping(변위 매핑)을 이용하는 것이죠.  Displacement Mapping   Displacement Mapping이란 Displacement Map을 이용해 물체를 구성하는 일련의 정점들을 재배치하는 것을 의미합니다. 가령, 평평한 격자의 물체가 있고 다음과 같은 두 개의 Displacement Map이 있다면 우리는 파도와 같은 현상을 만들어낼 수 있습니다. 하나는 큰 파도(저주파)를, 다른 하나는 작은 파도(고주파)를 재현합니다. 흰색일수록 위에 있으며, 검은색일수록 아래에 있게 됩니다.   이러한 Displacement Map들을 겹친 후에, 서로 다른 방향으로 움직이게 만들고 겹쳐진 값을 이용해서 Displacement Mapping을 한다면 저렴한 연산으로 파도와 같은 환상을 만들어낼 수 있습니다. 하지만 이 방법은 정적으로 파도가 만들어진다는 한계가 있습니다. 바람의 방향, 파도의 세기 등을 조절하기가 어렵죠. 조금 더 멋진 Displacement Map을 만들 수 있는 방법이 있을까요? Jerry Tessendorf의 'Simulating Ocean Water'   영화 프로듀서이자 교수인 Tessendorf는 그럴듯한 바다를 시뮬레이션할 수 있는 방법을 논문으로 정리해 제안하였습니다. 제가 다룰 내용을 간단히 요약하면 다음과 같습니다: 파도는 일종의 사인파와 코사인파의 합입니다. 따라서 푸리에 변환의 철학을 이용해서 복잡한 주기적 파
자세한 내용 보기

[코딩의탑] 5층: 포탈(Portal), 더 나아가기

이미지
2층에서 많은 부족함이 있었죠..   2층 에서 우리가 구현한 포탈은 다음과 같은 부족함이 있습니다: 포탈을 단순히 월드에 배치하기만 했으며, 포탈 건의 요구사항을 고려하지 않았습니다. 가령 포탈은 벽에 생성될 수 있어야 합니다. 플레이어의 포탈 이동만을 고려했습니다. 큐브 등 다른 오브젝트 역시 통과할 수 있어야 합니다. 포탈에 걸쳐있는 오브젝트는 포탈 양면에서 보일 수 있어야 합니다. 즉, 오브젝트의 복사가 이루어져야 합니다. Near plane clippng으로 인해 포탈에 들어가기 직전 카메라가 평면과 겹치는 순간, 포탈 평면의 뒷면 모습이 비춰집니다. 포탈에 비추는 플레이어의 모습이 3인칭으로 보여야 합니다. 효율적인 포탈 재귀 렌더링 방법이 필요합니다. 복습해봅시다. 벡터와 점의 변환   포탈 건너편으로 이동하는 효과를 주기 위해서, 우리는 적절히 오브젝트를 이동 및 회전시켜야 합니다. 속도 역시 적절한 방향으로 보존되어야 하죠. 포탈   먼저 위치와 속도는 3차원 벡터로 표현될 수 있습니다. 그리고 이것이 포탈과 포탈 사이에서 자연스럽게 이어져야 하죠. 마치 포탈이 붙어있는 것처럼요! 다음 그림을 참고해보세요. 블루 포탈과 오렌지 포탈은 서로가 위 방향 축을 기준으로 180도 회전한 상태에서 맞붙어있는 것처럼 느껴야 합니다. 블루 포탈과 오렌지 포탈   이는 각 포탈을 일종의 지역 좌표계로 생각해볼 수 있습니다. 포탈의 [앞 방향 벡터, 우측 방향 벡터, 위 방향 벡터]를 각각 [X, Y, Z]축으로 삼는 셈이죠. 우리는 마치 "이어져 있는" 환상을 선사해야 하므로, 한쪽 지역 좌표계의 좌표 값을 그대로 다른쪽 지역 좌표계의 좌표 값으로 자연스럽게 넘겨주면 됩니다. 다양한 방법이 있겠지만 성능을 위해, 각 축에 대한 내적의 값을 이용하도록 합시다. 각 축은 정규화되어 있고 수직이므로, 내적을 이용할 수 있습니다. 좌표계의 변환 소스 코드: APortal::TransformVectorToDestSpace(), TransformPoi
자세한 내용 보기