[Java] 자바로 프로그래밍 입문하기: 2.1. 정적 메소드(Static methods) (2)

 수학 함수 구현하기

  자바에서 이미 정의해놓은 정적 메소드들을 가져다쓰기만 하면 될까요? <Newton>에서 굳이 sqrt() 메소드를 구현해서 사용하는 것보다는, 자바 라이브러리에 있는 Math.sqrt()를 사용하는 것이 더 합리적입니다. 하지만 안타깝게도, 세상에는 무궁무진하게 수학 함수들이 많다는 것입니다. 자바에서는 아주 간단한 수학 함수들만 지원해줄 뿐이죠.

  예를 들어보죠. 100만명의 학생이 대학교에 입학하기 위한 시험을 치릅니다. 점수는 400점부터 1600점까지 다양한 선택 과목으로 시험을 봅니다. 체육 특기생은 820점을 넘겨야 하고, 특정 장학금을 받으려면 1500점을 넘겨야 된다고 해보죠. 체육 특기생이 될 수 없는 학생들의 비율은 얼마일까요? 또, 장학금을 받을 수 있는 학생들의 비율은 얼마일까요?

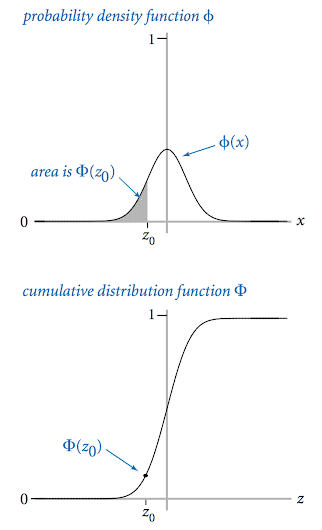
  두 개의 함수만 있다면 이 질문에 답변 할 수 있습니다. 가우시안(정규) 분포 함수는 종 모양의 그래프를 그리며, ϕ(x)=e−x2/2/
√2π의 형태로 이루어집니다. 누적 정규분포 함수 Φ(z)  는 정규 분포에서 수직선 x=z 왼쪽에 있는 넓이를 의미합니다. 이 함수들은, 우리의 예제에서 시험 점수의 분포를 정확하게 표현해냅니다. 

  하지만 자바의 Math 라이브러리에선 이런 정규 분포를 계산할 수 있는 메소드들을 지원하지 않으며, 우리는 필요에 의해 우리만의 메소드들을 만들어야 할 것입니다.

닫힌 형태(Closed-form, 방정식의 해를 해석적으로 표현할 수 있는 것, 예를 들어 2차방정식의 해는 근의 공식으로 표현될 수 있다.-옮긴 이)

  우리는 닫힌 형태의 수학 공식들을 쉽게 구현할 수 있습니다. ϕ를 구하는 것은, 자바 라이브러리의 지수 함수와 제곱근 함수를 이용해서 쉽게 구현할 수 있습니다. 따라서 정적 메소드 pdf()는 꽤나 구현하기 쉽죠.

닫히지 않은 형태(No closed-form)

  반면, 함수값을 계산하기 위해 우리는 꽤나 복잡한 알고리즘을 사용해야 합니다. 이 경우 Φ가 됩니다. 이러한 알고리즘은 테일러 급수의 근사치를 이용할 수 있습니다. 이는 수백 년동안 쌓인 수학적 경험을 토대로 하며, 수학 함수의 구현은 아주 신중하게 해야합니다. 하여튼, 다음과 같은 식으로 나타낼 수 있습니다.

Φ(z)==∫z−∞ϕ(x)dx12+ϕ(z)(z+z33+z53⋅5+z73⋅5⋅7+…)

프로그램 2.1.2: Gaussian functions

public class Gaussian { // return pdf(x) = standard Gaussian pdf public static double pdf(double x) { return Math.exp(-x*x / 2) / Math.sqrt(2 * Math.PI); } // return pdf(x, mu, signma) = Gaussian pdf with mean mu and stddev sigma public static double pdf(double x, double mu, double sigma) { return pdf((x - mu) / sigma) / sigma; } // return cdf(z) = standard Gaussian cdf using Taylor approximation public static double cdf(double z) { if (z < -8.0) return 0.0; if (z > 8.0) return 1.0; double sum = 0.0, term = z; for (int i = 3; sum + term != sum; i += 2) { sum = sum + term; term = term * z * z / i; } return 0.5 + sum * pdf(z); } // return cdf(z, mu, sigma) = Gaussian cdf with mean mu and stddev sigma public static double cdf(double z, double mu, double sigma) { return cdf((z - mu) / sigma); } // Compute z such that cdf(z) = y via bisection search public static double inverseCDF(double y) { return inverseCDF(y, 0.00000001, -8, 8); } // bisection search private static double inverseCDF(double y, double delta, double lo, double hi) { double mid = lo + (hi - lo) / 2; if (hi - lo < delta) return mid; if (cdf(mid) > y) return inverseCDF(y, delta, lo, mid); else return inverseCDF(y, delta, mid, hi); } // return phi(x) = standard Gaussian pdf @Deprecated public static double phi(double x) { return pdf(x); } // return phi(x, mu, signma) = Gaussian pdf with mean mu and stddev sigma @Deprecated public static double phi(double x, double mu, double sigma) { return pdf(x, mu, sigma); } // return Phi(z) = standard Gaussian cdf using Taylor approximation @Deprecated public static double Phi(double z) { return cdf(z); } // return Phi(z, mu, sigma) = Gaussian cdf with mean mu and stddev sigma @Deprecated public static double Phi(double z, double mu, double sigma) { return cdf(z, mu, sigma); } // Compute z such that Phi(z) = y via bisection search @Deprecated public static double PhiInverse(double y) { return inverseCDF(y); } // test client public static void main(String[] args) { double z = Double.parseDouble(args[0]); double mu = Double.parseDouble(args[1]); double sigma = Double.parseDouble(args[2]); StdOut.println(cdf(z, mu, sigma)); double y = cdf(z); StdOut.println(inverseCDF(y)); } }

% java Gaussian 620 1019 209
0.17050966669132111

% java Gaussian 1500 1019 209
0.9693164637363663

% java Gaussian 1500 1025 231
0.9601220907365469

  Deprecated 된 메소드는, 이전에는 있었으나 현재에 와서는 문제가 있어 다른 메소드로 대체된 경우입니다. 즉 사용하지 않으므로 알 필요는 없으며, 같은 기능을 하는 메소드가 다른 이름으로 있을 것입니다. (개정이 되면서 코드가 수정되었습니다-옮긴 이)

코드를 정리하기 위해 정적 메소드를 사용하기

  수학 함수를 넘어, 입력 값을 기반으로 결과값을 처리하는 것은 어떤 프로그램의 제어 흐름을 구성하든 간에 중요합니다. 좋은 프로그래머라면 동의하지 않을 수 없는 아주 간단하고 굉장히 중요한 원칙에 대해서 다시 이야기해볼까 합니다. "프로그램에서 작업의 단위를 나눌 수 있다면, 그렇게 해야 합니다."

  함수는 계산 작업의 자연스럽고 보편적인 표현입니다. 1.1절에서 했던 이야기를 기억하시나요? 자바 프로그램은 문자열(명령행 인자)을 받아서 또 다른 문자열(결과)을 출력하는 함수에 불과하지 않는다고 했습니다. 이 관점은 그 자체로 다양한 깊이의 프로그램들을 나타낼 수 있습니다. 특히, 프로그램이 길면 길수록 자바의 대입문, 조건문, 반복문들보다, 함수들로 나타내지는 것이 훨씬 자연스럽습니다.

프로그램 2.1.3: Coupon collector (revisited)

public class Coupon { public static int uniform(int N) { // Generate a random integer between 0 and N-1. return (int) (Math.random() * N); } public static int collect(int N) { // Collect coupons until getting one of each value. boolean[] found = new boolean[N]; int cardcnt = 0, valcnt = 0; while (valcnt < N) { int val = uniform(N); cardcnt++; if (!found[val]) valcnt++; found[val] = true; } return cardcnt; } public static void main(String[] args) { // Print the number of coupons collected // to get N different coupons. int N = Integer.parseInt(args[0]); int count = collect(N); StdOut.println(count) ; } }

% java Coupon 1000
6522

% java Coupon 1000
6481

% java Coupon 1000000
12783771

  <Coupon>은 <프로그램 1.4.2, CouponCollector>의 새로운 버전입니다. 계산 작업들을 좀 더 분할했죠. 여러분은 <CouponCollector>를 세 가지의 작업으로 나눌 수 있을 것입니다:

• N이 주어지면, 무작위의 쿠폰 값을 생성합니다.
• N이 주어지면, 쿠폰 모으기 시뮬레이션을 실행합니다.
• N을 명령행으로부터 얻고, 계산 후 결과를 출력합니다.

  이런 구성이라면, uniform()을 변경하거나 main()을 변경해도 collect()에 미칠 영향에 대해 걱정하지 않아도 됩니다. 예를 들어, uniform()을 수정해 다른 방식으로 난수를 생성할 수 있고, main()을 수정해 여러 입력을 받거나 여러 번 시행을 하게끔 수정할 수도 있죠. 하지만 collect()는 여전히 자기 일만 열심히 하면 된다는 사실에 주목하세요.

  정적 메소드를 이용하는 것은, 각 컴포넌트의 구현으로부터 서로를 독립적으로 만들거나 캡슐화(encapsulates) 시킵니다. 보통 프로그램은 각 메소드의 분할으로 얻을 수 있는 이점을 극대화 하기 위해, 수많은 독립적 컴포넌트를 갖고 있습니다. 앞으로도 이런 것들이 왜 좋은지에 대해 계속 배워나갈 것이며, 여러분은 함수로 작업을 쪼개는 것이 좋은 것이라는 점만 기억하세요. "프로그램에서 작업의 단위를 나눌 수 있다면, 그렇게 해야 합니다."

배열을 이용하는 정적 메소드 구현하기

  정적 메소드는 인자나 반환값으로 배열을 사용할 수 있습니다. 이 기능은 챕터 3에서 이야기 할 자바 객체 지향에서의 특수한 경우입니다. 하지만 이를 지금 미리 다뤄보는 이유는, 메커니즘을 이해하고 사용하기 쉬우며 많은 양의 자료를 다루는 숫자 문제들로부터 간편한 해답을 제시해주기 때문입니다. 

배열인 인자

  정적 메소드가 배열을 인자로 받는다는 것은, 같은 자료형인 많은 수의 값들을 다루는 함수를 구현한다는 것입니다. 예를 들어, 다음 정적 메소드는 주어진 double 값들의 배열을 인자로 받아 평균을 계산합니다.

public static double mean(double[] a) { double sum = 0.0; for (int i = 0; i < a.length; i++) sum = sum + a[i]; return sum / a.length; }

  사실 우리는 이미 배열을 인자로 사용해왔었습니다. main()은 정적 메소드이면서 문자열 배열을 인자로 받고 아무것도 반환하지 않는 메소드입니다. 편리하게도 자바 시스템은 java 커맨드 이후에 입력하는 것들을 모아서 args[]에 담아 main()을 호출합니다.(대부분의 프로그래머들은 매개변수의 이름으로 args를 씁니다만, 다른 이름을 써도 상관은 없습니다)

배열의 부작용(Side effects with arrays)

  배열로 인자를 받는 정적 메소드의 경우 종종 부작용을 일으킵니다. 배열의 값을 변경하게 되죠. 예를 들어 다음 메소드는 주어진 배열 내의 두 값의 위치를 서로 바꿉니다. 이와 비슷한 코드를 1.4절에서 본 적이 있었죠.

public static void exch(String[] a, int i, int j) { String t = a[i]; a[i] = a[j]; a[j] = t; }

  하지만 상식적으로 생각해보면 이상합니다. 분명 매개변수로 받은 것들은 해당 메소드 내에서만 사용되고, 메소드를 실제 호출한 곳에서는 어떤 변화도 일어나지 않아야 합니다. 우리가 매개변수로 받은 i와 j를 아무리 변경해도 exch()를 호출한 곳에서는 아무 일도 일어나지 않을 것인데, 어째서 배열은 바뀌게 될까요?

  이는 우리가 이전에 배웠던 자바의 배열 구조로 거슬러 올라가게 됩니다. 혹 기억이 나지 않는다면, 1.4절을 참고하세요. exch()의 매개변수 a는 '배열'을 참조하고 있지, '배열의 값'을 참조하는 것이 아니기 때문입니다. 정적 메소드에게 배열로 인자를 주는 것은, 곧 그 배열을 다룰 수 있는 기회를 주는 것입니다. 배열의 주소를 넘겨주는 것이므로, 단순히 복사가 아닙니다!

  이 예제들은 전부, 자바에서 배열을 전달하는 메커니즘은 배열의 내용에 대하여 call-by-reference(참조에 의한 호출) 메커니즘이라는 기초적인 사실을 드러냅니다. 기본 타입 인자들과는 달리, 배열에 대한 변경은 그 즉시 클라이언트 프로그램에 반영됩니다. 

배열인 반환값

  인자로 받은 배열을 정렬하거나, 섞는 등 배열을 변경하는 메소드는 배열에 대한 참조를 다시 반환할 필요가 없습니다. 왜냐하면 배열을 복사한 것이 아니라, 실제 연결된 배열의 내용을 바꾼 것이기 때문입니다. 즉, 부작용을 일으킨 셈이죠.

  하지만 배열을 반환하는 것이 유용한 상황도 굉장히 많습니다. 그 중 가장 중요한 것은, 동일한 자료형의 여러 값을 반환하기 위해 배열을 생성하여 반환해주는 상황입니다. 예를 들어, 다음 정적 메소드는 인자로 진동수와 시간을 주면 해당하는 사인파를 샘플링해서 반환합니다. 

public static double[] tone(double hz, double t) { int sps = 44100; int N = (int) (sps * t); double[] a = new double[N+1]; for (int i = 0; i <= N; i++) a[i] = Math.sin(2 * Math.PI * i * hz / sps); return a; }

  이 코드에서, 배열의 크기는 시간에 비례합니다. t가 주어지면, 배열의 크기는 44100*t가 됩니다. 이런 정적 메소드를 이용하면, 단일 개체로 이루어진 음악을 만들 수 있습니다.

예제: 화음(Superposition of sound waves)

  우리는 1.5절에서 소리를 만드는 프로그램에 대해 공부한 적이 있습니다. 하지만 이는 단순한 소리를 만드는 데에 그치므로, 좀 더 악기스러운 소리를 만들어낼 필요가 있습니다.

코드와 화성(Chords and harmonics)

  아마 <PlayThatTune> 프로그램을 통해 듣는 소리는, 여러분이 평소에 들었던 악기의 소리와는 많이 달랐을 것입니다. 기타 줄의 소리는 기타의 몸체나, 여러분이 있는 방의 벽 등을 통해 공명합니다. 이런 것들은 전부 사인파로 표현될 수 있습니다.

  대부분의 악기는 여러분이 원하든 원하지 않든 화성을 만들어냅니다. 여러분이 직접 코드를 잡아 연주할 수도 있고, 한 음만 연주하여도 알게 모르게 옥타브의 음들이 공명하게 됩니다. 이 역시 화음이죠.

  여러 음을 조합하기 위해서, 우리는 간단히 중첩(superposition)을 이용해볼까 합니다. 위아래로 한 옥타브의 음을 함께 연주하는 것이죠. 서로 다른 주기의 사인파를 중첩할 때, 우리는 임의의 복잡한 파동을 얻을 수 있습니다. 19세기에 수학자들은 이런 복잡한 파동을 사인파와 코사인파의 합으로 표현할 수 있는 방법을 만들어냈습니다. 바로 푸리에 급수(Fourier series)입니다.

중첩(Superposition)

  우리가 배열에 있는 숫자로 각 지점에 대해 샘플링된 음파를 표현해냈으므로, 중첩은 구현하기 쉽습니다. 각 해당하는 지점에 필요한 음을 쌓아주기만 하면 되는 것이죠. 두 음을 어떻게 합칠 수 있을까요? 다음 코드조각을 통해 살펴봅시다. awt와 bwt는 각 음파에 대한 상대 가중치입니다. 무조건 반반으로 음을 섞으면 재미 없으니까요.

double[] c = new double [a. length]; for (int i = 0; i < a.length; i++) c[i] = a[i]*awt + b[i]*bwt;

프로그램 2.1.4: Play that Tune(revisited)

public class PlayThatTuneDeluxe { // return weighted sum of two arrays public static double[] sum(double[] a, double[] b, double awt, double bwt) { // precondition: arrays have the same length assert a.length == b.length; // compute the weighted sum double[] c = new double[a.length]; for (int i = 0; i < a.length; i++) { c[i] = a[i] * awt + b[i] * bwt; } return c; } // create a pure tone of the given frequency for the given duration public static double[] tone(double hz, double duration) { int n = (int) (StdAudio.SAMPLE_RATE * duration); double[] a = new double[n + 1]; for (int i = 0; i <= n; i++) { a[i] = Math.sin(2 * Math.PI * i * hz / StdAudio.SAMPLE_RATE); } return a; } // create a note with harmonics of the given pitch and duration // (where 0 = concert A) public static double[] note(int pitch, double duration) { double hz = 440.0 * Math.pow(2, pitch / 12.0); double[] a = tone(hz, duration); double[] hi = tone(2 * hz, duration); double[] lo = tone(hz / 2, duration); double[] h = sum(hi, lo, 0.5, 0.5); return sum(a, h, 0.5, 0.5); } // read in notes from standard input and play them on standard audio public static void main(String[] args) { // read in pitch-duration pairs from standard input while (!StdIn.isEmpty()) { int pitch = StdIn.readInt(); double duration = StdIn.readDouble(); double[] a = note(pitch, duration); StdAudio.play(a); } } }

  <프로그램 2.1.4>는 좀 더 현실적인 소리를 만들어냅니다. 네 개의 함수로 구성이 되어있습니다.

• 주어진 진동수(frequency)와 시간으로, 순수한 음을 생성합니다.
• 주어진 두 음파와 상대 가중치로, 두 음파를 합칩니다.
• 주어진 음(pitch)과 시간으로, 화성음을 만들어냅니다. (음을 진동수로 치환하는 작업도 포함합니다)
• 일련의 음/시간 쌍을 표준 입력으로부터 읽어들입니다.

  이 작업들은 각각 서로 의존하는 기능으로, 우리가 원하는 기능을 충분히 구현할 수 있습니다. 지금까지 우리의 함수 사용은, 단순히 보기에 좋으려고 사용한 것에 불과했습니다. 예를 들어 <프로그램 2.1.1-2.1.3>의 제어 흐름은 굉장히 간단하죠. 각 함수가 필요한 자리에서 한 번 호출될 뿐입니다.

  반면 <PlayThatTuneDelxue>는 함수를 정의함으로서 프로그램의 흐름을 효과적으로 조직할 수 있음을 입증합니다. 각 함수가 여러 번 호출되면서, 본래에는 여러 번 중복해 작성해야 했을 것을 효율적으로 처리하고 있죠. note()를 보면, tone()을 세 번 호출하고 sum()을 두 번 호출합니다. 

  만약 정적 메소드라는 것이 없었다면, 해당하는 내용을 그대로 여러 번 중복해서 작성했었을 것입니다. 마치 반복문처럼, 메소드는 간단하지만 중요한 효과를 가져옵니다. (메소드에 정의된)일련의 구문을 여러 번 손쉽게 사용할 수 있게 하는 것입니다. 

  정적 메소드는 우리에게 자바 언어를 확장할 수 있게 만들어줍니다. 이제는 자바 프로그램에서, 내부적으로 또다른 정적 메소드를 호출하는 정적 메소드의 집합에 대해 생각해볼 필요가 있습니다.

  "프로그램에서 작업의 단위를 나눌 수 있다면, 그렇게 해야 합니다." 이는 코드를 이해하기 쉽게 만들고, 유지보수 및 오류를 해결하는데 도움이 됩니다. 다음 절에서 우리는 다른 프로그램에서 정의된 정적 메소드들을 활용하는 방법에 대해 이야기 해볼 것입니다.

끝.